КВАДРАТТЫК ТЕҢДЕМЕНИ ЧЫГАРУУНУН ЭҢ КЫСКА ЖОЛУ

• Түшүндүрмө
• Квадраттык теңдемени чыгаруунун үч жолу
• Жаңы методго келтирүүгө мисалдар

ТҮШҮНДҮРМӨ

ах²+вх+с=0 квадраттык теңдемесинде а=в²; с= -2 шарты аткарылган учурдагы квадраттык теңдемени чыгаруунун эң  кыска жолун сунуштайм.

Эгерде, жогорудагы шарттар аткарылса жана в санынын  белгиси оң болсо, анда белгисиздин тамырлары:

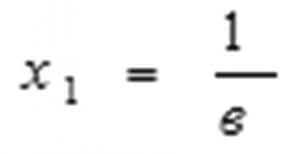
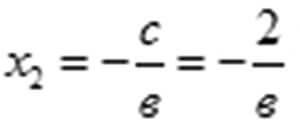
барабар  болот.

 Эгерде, в санынын  белгиси  терс  болсо, анда  белгисиздин тамырлары:

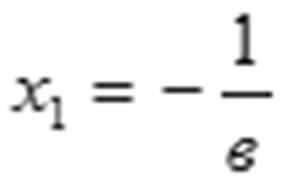
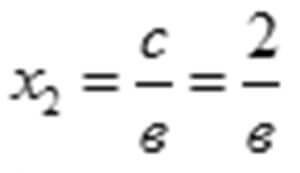                   барабар   болот.

Максатым –  аз  убакыт ичинде белгисиз  сандын  тамырын оозеки  табуу  болуп эсептелет.

Интернет  булактарынан  караганда  ушул жолдун шартына окшош америкалык окумуштуунун Sultanov’дун методу көрсөтүлгөн, ал методдо белгилеп алуу жолун колдонуп тамырын таап, андан кийин квадраттык үч  мүчөнү сызыктуу көбөйтүүчүлөргө ажыратуу менен белгисиздин тамырларын тапкан.

Жаңы  табылган метод  Sultanov’дун  методуна караганда жеңил жана  кыска, оозеки  чыгаруунун жолу  болуп  эсептелинет.

Бул кол жазмамда (монографиямда) жаңы табылган методдун тууралыгын жана ыңгайлуулугун далилдөө үчүн аны башка методдор  менен  салыштырып  чыгарылган мисалдарды жана  ушул жаңы  методго  келтирүүнүн  жолдорун  көрсөттүм.

36 х²+6х-2=0 квадраттык теңдемени чыгаруунун үч жолу

а)  ах²+вх+с=0;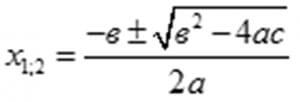 

квадраттык теңдеменин  тамырын  табуу формуласы менен  чыгаруу

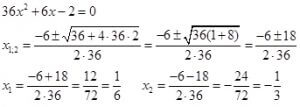
б) Sultanov’дун методу боюнча чыгаруу

36 х²+6х-2=0  белгилеп алуу жолун колдонгон у=6х у²+у-2=0 теңдеме нөлгө барабар болсун үчүн   у=1 болуш керек экендигин оозеки аныктагандан кийин, квадраттык үч мүчөнү сызыктуу көбөйтүүчүлөргө ажыратып

(у-1)(у+2)=0 у₁=1 у₂=-2

андан кийин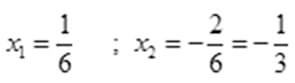

тамырларын тапкан.

 в)  Жаңы метод менен чыгаруу

ах²+вх+с=0  квадраттык теңдемеде а=в²; с= – 2 шарты аткарылган учурда чыгаруунун эң кыска жолу көрсөтүлгөн.

Эгерде жогорудагы шарттар аткарылса жана в санынын  белгиси оң болсо, анда белгисиздин тамырлары:

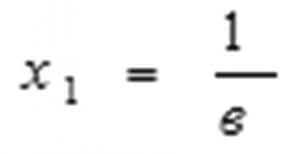
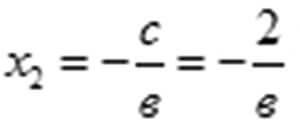                    (1)   барабар  болот.

Эгерде  в  санынын  белгиси  терс  болсо, анда  белгисиздин тамырлары:

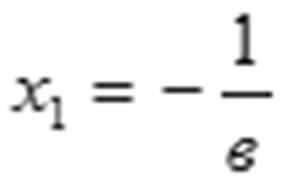
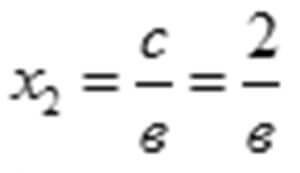      (2)   барабар   болот.

36 х²+6х-2=0  жогорку шарт аткарылгандыктан (1) учурдагы шарт менен

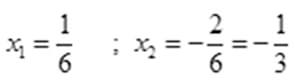
оозеки   жообун берсе болот.

 Текшерүү:

теңдемеге биринчи жана экинчи тамырын коюп текшергенимде жооптун  туура экендиги аныкталды.

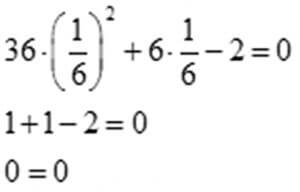
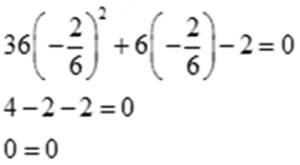
Жаңы методго келтирүүгө мисалдар:

№1    50х² -10х-4=0   квадраттык  теңдемеде  а=в² ; с=-2 шарты аткарылыш үчүн 2ге бөлөбүз.

50х² -10х-4=0

25х² -5х -2=0 коюлган шартка келтирилгенден кийин тамырын табабыз,

анда х₁ = -1/5; х₂ = 2/5     текшерүү:

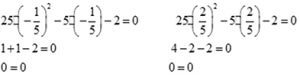
№2

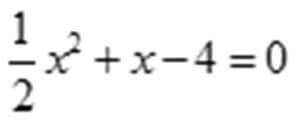 жаңы методго келтириш үчүн теңдемени 2ге бөлөбүз шарты аткарылгандан кийин жообу:

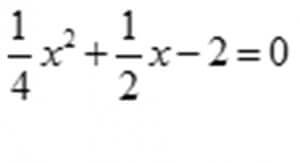
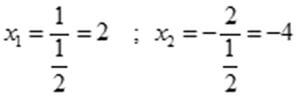
Текшерүү:

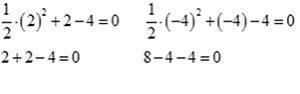
0=0                                 0=0

№3   2х²-х-1=0 жаңы методго келтириш үчүн теңдемени 2ге көбөйтөбүз, анда теңдеме төмөнкүдөй болуп калат.

4х²-2х-2=0  шарт аткарылгандан кийин (2) формуланы колдонуп

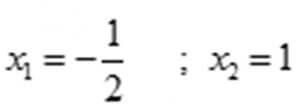
тамырларын аныктайбыз.

Текшерүү:

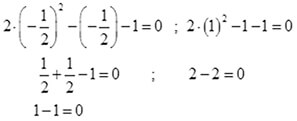
Мамбеталиева Күльджандын методу боюнча «Бөлүмдөрү окшош көбөйтүүчүгө ажырай турган сандардын жалпы бөлчөгүн табуу»

Бул метод 2002-жылы ойлоп табылган, 15 жылдан бери окуучуларга түшүндүрүүдө колдонуп жүрөм, жыйынтыгында окуучулар бат жана оңой кабылдашат.

Максаты:  Бөлчөктүү сандардын жалпы бөлчөгүн аз убакыт ичинде ылдам (оңой) табуу.

Бөлүмдөрү окшош көбөйтүүчүгө ажырай турган       сандардын жалпы бөлчөгүн табуу жолу.

М:        

Түшүндүрмө: Бөлчөк сандардын бир көбөйтүндүсү окшош болгондой кылып ажыратабыз, окшош көбөйтүндүнү кашаанын сыртына чыгарабыз, кашаанын ичиндеги бөлчөктөрдүн жалпы бөлүмүн табабыз.

Кашаанын сыртына чыккан сан менен көбөйтүп коебуз.

Ушул эсепти башка жол менен чыгаралы

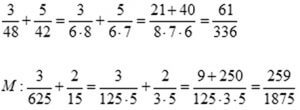
Бөлчөк сандардын бир көбөйтүндүсү окшош болгондой кылып ажыратабыз, жалпы бөлчөк үчүн эки бөлчөктөн окшош эмес көбөйтүүчүнү жана окшош көбөйтүүчүнүн бирин жазабыз. Жалпы бөлчөк көбөй-түүчүлөргө ажыраган боюнча калтырылат, себеби  аны ар бир бөлчөккө бөлүп,  тийиндини оңой табууга оңтойлуу болот.  Тийиндини алыш үчүн жалпы бөлчөктөгү көбөйтүүчүлөрдүн ичинен биринчи жана экинчи бөлчөктөгү көбөйтүүчүлөргө жетпеген санды таап (ушул сан тийинди болот), бөлчөктүн алымындагы сан менен көбөйтүп кошуу же алуу амалдарын жүргүзөбүз.