«ЮНЫЕ ПИФАГОРЫ В МИРЕ ТЕХНИКИ»
- 06.12.2017
- 2

Уважаемые родители!
Сегодня, в век информационного общества, возрастает роль естественно-математических знаний. Одной из наиболее значимых форм повышенной математической подготовки являются математические олимпиады.
Уже который год Республиканская детская инженерно-техническая академия «Алтын туйун» собирает юных любителей математики в рамках участия в математической олимпиаде. Республиканская математическая олимпиада «Юные пифагоры в мире техники» — ежегодное открытое соревнование по математике для школьников Кыргызстана. Олимпиада проводится по трем возрастным группам: среди школьников 3-4-х классов, 5-6-х классов и 7-8-х классов на кыргызском и русском языках.
В 2017-2018 году Республиканская олимпиада по математике «Юные пифагоры в мире техники», проводимая Республиканской детской инженерно-технической академией «Алтын туйун», пройдет в три тура: дистанционный, региональный и заключительный.
С 1 декабря 2017 стартует дистанционный тур, который продлится до 20 января 2018 года. На данном этапе олимпиады учащимся необходимо решить 10 задач.
Решение задач должно быть записано подробно, математически грамотно оформлено, все чертежи и схемы должны быть выполнены карандашом. Приветствуется решение задач несколькими способами.
Решения задач должны быть представлены в тонкой ученической тетради, на обложку которой наклеивается анкета участника (см. Приложение 1), где указывается Ф.И.О., почтовый адрес, телефон, номер и адрес школы, класс участника, а также Ф.И.О. директора школы, учителя, или того, с кем занимается ученик подготовкой к олимпиаде. Работа выполняется учеником самостоятельно, без посторонней помощи. За нарушение этого правила участник может быть дисквалифицирован. Решения задач необходимо прислать по адресу: 720017, г. Бишкек, пр. Манаса, 1, РДИТА «Алтын туйун», РМО. Родители школьников г. Бишкек и Чуйской области могут самостоятельно привезти тетради с решениями (в конверте, но без почтовой марки) в РДИТА «Алтын туйун».
Итоги дистанционного тура будут подведены 1 февраля 2018 года, списки участников следующего регионального тура будут опубликованы в газете «Кут билим» и на сайте РДИТА «Алтын туйун». Желаем успеха!
Приложение 1.
| Фамилия | |||||||||||||
| Имя, Очество | |||||||||||||
| Класс, № школы | |||||||||||||
| Домашний адрес | |||||||||||||
| Область (регион) | |||||||||||||
| Телефон, E-mail | |||||||||||||
| Телефон, ФИО директора | |||||||||||||
| ФИО учителя и (или) того, с кем занимаетесь математикой | |||||||||||||
| Региональный тур | Номер | 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | Сумма | Проверил |
| Баллы | |||||||||||||
Задания дистанционного тура
Республиканской олимпиады по математике
«Юные пифагоры в мире техники»
3-4 класс. (2017-18 г.)
- На свой день рождения фрекен Бок испекла огромный торт. Известно, что Малыш и торт весили столько же, сколько Карлсон и фрекен Бок. После того, как торт съели, Карлсон весил столько же, сколько фрекен Бок и Малыш. Докажите, что кусок торта, который съел Карлсон, весит столько же, сколько весила фрекен Бок до своего дня рождения.
- Старушка поднялась с 1-го этажа на 5-ый за 5 минут. За сколько минут она поднимется с 1-го этажа на 9-ый, если будет идти с той же скоростью?
- В бутылке было 250 мл молока. В первый день Паша выпил пятую часть всего молока. Во второй день он выпил четвертую часть того, что осталось. Все остальное допила Оля. Кто выпил больше молока и насколько?
- В шкафу у Пьеро свалены в кучу 12 пар белых и 10 пар черных носков. Пьеро вынимает один носок за другим – с закрытыми глазами. Сколько носков он должен вынуть, чтобы надеть пару одного (любого) цвета? Белого цвета? Чёрного цвета?
- В буфете кукольного театра Пьеро заплатил 2 золотых монеты за мороженое и 2 пирожных. А Мальвина заплатила 5 золотых монет за 3 мороженых и 4 пирожных. Сколько пирожных сможет купить Буратино на 3 золотые монеты?
- Вася посчитал, что если каждая девочка принесёт по 3 рубля, а каждый мальчик по 5 рублей, все 30 учащихся соберут 122 рубля. Сколько в классе мальчиков и сколько девочек?
- В мешке 24кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9кг гвоздей?
- Мальчик по чётным числам всегда говорит правду, а по нечётным всегда врёт. Как-то его три ноябрьских дня подряд спрашивали: «Как тебя зовут?». На первый день он ответил: «Андрей», на второй: «Борис», на третий: «Виктор». Как зовут мальчика?
- Кот Матроскин прикинул, что он может выложить пол квадратной комнаты квадратной плиткой, и ему не понадобится ни одну из них разрезать. Сначала он положил плитки по краям комнаты, и на это у него ушло 84 плитки. Сколько всего ему надо иметь плиток, чтобы покрыть весь пол?
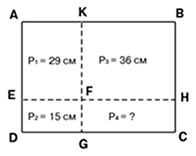
- Прямоугольник ABCD разделили двумя прямолинейными разрезами на четыре прямоугольника. Известно, что периметр прямоугольника AKFE равен 29 см, периметр прямоугольника EFGD равен 15 см, а периметр прямоугольника KBHF равен 36 см. Найдите периметр прямоугольника FHCG. Ответ объясните.
Задания дистанционного тура
Республиканской олимпиады по математике
«Юные пифагоры в мире техники»
5- 6 класс. (2017-18 г.)
- У Маши есть 10 красных и зелёных яблок, которые она разложила на 5 тарелочек, по два яблока на каждую. Оказалось, что ровно половина красных яблок лежит на тарелочках вместе с зелёными. Может ли Маша переложить яблоки по-другому: так, чтобы половина зелёных лежала вместе с красными
- Нурбек получил за год несколько оценок по математике, всего их было меньше 100. Ровно треть из них – «тройки», ровно четверть – «четверки», ровно пятая часть – «пятерки». А сколько Нурбек получил «двоек». Назовите точное количество.
- Саша обратил внимание на номер автомашины, подъехавшей к его дому: СТО 85—87. Интересно, если прибавить к первому числу цифры второго, то получится 85 + 8 + 7 = 100, и если прибавить ко второму числу цифры первого, то тоже получится 87 + 8 + 5 = 100. А сколько всего таких номеров?
- Начнём считать пальцы на левой руке. 1-м будет большой, 2-м — указательный, 3-м — средний, 4-м — безымянный, 5-м — мизинец, 6-м — снова безымянный, 7-м — средний, 8-м — указательный, 9-м — большой, 10-м — указательный и.т.д.
Какой палец будет 1979-м?
- Найдите все такие двузначные числа, которые делятся на каждую из цифр в их записи.
- У Пети есть четыре орешка. Он всеми возможными способами брал по три орешкаи взвешивал их на весах. Получилось 9 г, 14 г, 16 г и 18 г. Сколько весил каждый орешек?
- Из своих норок одновременно навстречу друг другу выскочили 2 зайчонка. Через 3 мин они столкнулись нос к носу и, перепугавшись, бросились в обратные стороны с такими же скоростями. Через 30 сек после встречи, зайчата остановились, и расстояние между ними было 21 м. Скорость одного зайчонка на 6 м/мин больше скорости другого. На каком расстоянии от своей норки оказался более быстрый зайчонок?
- Жук ползает по клетчатой плоскости, сторона клетки которой равна 1 см. Он выполз из точки О, прополз вверх 1 см, повернул вправо и прополз 2 см, потом вновь повернул направо и прополз 3 см, потом – 4 см, и т. д.. Сколько раз он при этом был на расстоянии 2 см от точки О?
- Кот Матроскин принёс с базара несколько яблок и хвастается Шарику: «Я купил в четыре раза больше яблок, чем ты вчера, но заплатил за каждое яблоко вдвое меньше». Сколько денег заплатил Матроскин, если Шарик истратил на яблоки 75 рублей?
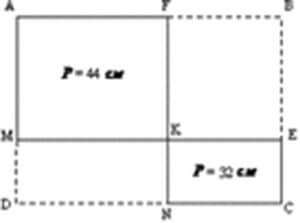
- Прямоугольник ABCD разделили двумя прямолинейными разрезами на четыре прямоугольника. Известно, что периметр прямоугольника AFKM равен 44 см, а периметр прямоугольника KECN равен 32 см. Найдите периметр прямоугольника ABCD. Ответ объясните.
Задания дистанционного тура
Республиканской олимпиады по математике
«Юные пифагоры в мире техники»
7-8 класс. (2017-18 г.)
- Каждый из 10 гномов либо всегда говорит правду, либо всегда лжет. Известно, что каждый из них любит ровно один сорт мороженого: сливочное, шоколадное или фруктовое. Сначала Белоснежка попросила поднять руки тех, кто любит сливочное мороженое, и все подняли руки, потом тех, кто любит шоколадное мороженое – и половина гномов подняли руки, потом тех, кто любит фруктовое мороженое – и руку поднял только один гном. Сколько среди гномов правдивых?
- Саша, Лёша и Коля одновременно стартовали в забеге на 100 м. Когда Саша финишировал, Лёша находился в десяти метрах позади него, а когда финишировал Лёша — Коля находился позади него в десяти метрах. На каком расстоянии друг от друга находились Саша и Коля, когда Саша финишировал? (Предполагается, что все мальчики бегут с постоянными, но, конечно, не равными скоростями.)
- В школе 350 учеников и 175 парт. Ровно половина девочек сидит за одной партой с мальчиками. Можно ли пересадить учеников так, чтобы ровно половина мальчиков сидела за одной партой с девочками?
- Маугли попросил обезьян принести ему орехов. Обезьяны набрали поровну орехов и понесли их Маугли. По дороге они поссорились, и каждая обезьяна бросила в каждую по ореху. В результате у Маугли досталось лишь 33 ореха. По сколько орехов собрали обезьяны? Известно, что каждая обезьяна принесла больше одного ореха.
- Возьмем два двузначных числа и перемножим их. Произведение обозначим через А. Теперь в каждом из сомножителей переставим цифры и перемножим полученные числа. Полученное число обозначим через В.
Докажите, что число А — В делится на 99.
- Есть 24 палочки. Длина первой палочки – 1 см, второй – 2 см, …, двадцатьчетвёртой – 24 см (длина каждой следующей палочки на 1 см больше длины предыдущей). Как, использовав все эти палочки, составить три различных квадрата? Ломать палочки нельзя, каждая палочка должна входить только в один квадрат.
- Петя тратит 1/3 своего времени на игру в футбол, 1/5 — на учебу в школе, 1/6 — на просмотр кинофильмов, 1/7 — на решение олимпиадных задач, и 1/3 — на сон. Можно ли так жить?
- У колхозника было несколько одинакового веса поросят и несколько ягнят также одинакового веса. Пионер спросил колхозника, сколько весит один поросенок и один ягненок. Колхозник ответил, что 3 поросенка и 2 ягненка весят 22 кг, а 2 поросенка и 3 ягненка весят 23 кг. Как узнать, сколько весит один поросенок и сколько весит один ягненок?
- Три друга сделали по одному заявлению про целое числох. Петя: «Число х больше 4, но меньше 8». Вася: «Число х больше 6, но меньше 9». Толя: «Число х больше 5, но меньше 8». Найдите число х, если известно, что двое из друзей сказали правду, а третий солгал. Нужно не только проверить, что найденное число годится, но и объяснить, почему другие варианты ответа невозможны.
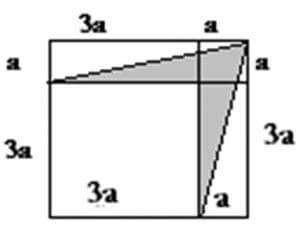
- Найти площадь заштрихованной фигуры внутри квадрата на рисунке. Сторона квадрата равна 4a.
Комментарии